Excel數(shù)據(jù)分析工具庫是一個非常強(qiáng)大的工具,，可以滿足基本的統(tǒng)計分析。本文介紹了用Excel數(shù)據(jù)分析工具庫中的回歸進(jìn)行回歸分析,。

本節(jié)中的知識點：

Excel數(shù)據(jù)分析工具庫-回歸線性回歸和非線性回歸簡單線性回歸和多元線性回歸logistic回歸

一,、什么是回歸分析？

1.定義

確定兩個或多個變量之間相關(guān)性的統(tǒng)計分析方法,。通過對數(shù)據(jù)之間相關(guān)性分析的研究,，進(jìn)一步建立自變量(i=1，2,，3，…)與因變量Y之間的回歸函數(shù)關(guān)系,，即回歸分析模型,，從而預(yù)測數(shù)據(jù)的發(fā)展趨勢。

2.分類

根據(jù)涉及的變量個數(shù),，分為單變量回歸和多變量回歸分析,；根據(jù)因變量的個數(shù)，可分為簡單回歸分析和多元回歸分析,；根據(jù)自變量和因變量之間的關(guān)系類型,，可分為線性回歸分析和非線性回歸分析。

第二,，線性回歸

1.簡單線性回歸

簡單線性回歸也叫一元線性回歸,，即回歸模型中只有一個自變量和一個因變量，其回歸方程可表示為：

Y=a bx

其中y為因變量，x為自變量,，a為常數(shù),，b為斜率。

這是隨機(jī)誤差,。

2.最小二乘法：

如何確定參數(shù)A和B,，應(yīng)該用最小二乘法來實現(xiàn)。通過最小化誤差的平方和,，找到數(shù)據(jù)的最佳函數(shù)匹配,，即觀測點與估計點距離的平方和最小。

3,、線性回歸分析的步驟：

確定自變量和因變量,，繪制散點圖，確定回歸模型的類型,，估計模型參數(shù),，建立回歸模型：用最小二乘法估計模型參數(shù)，檢驗回歸模型,，用回歸模型進(jìn)行預(yù)測,。

4.多元線性回歸

定義：一個因變量和多個自變量的線性回歸問題是一個變量線性回歸的推廣?；貧w方程可以寫成：

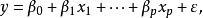
最小二乘法也被用來估計多元線性回歸方程中的回歸系數(shù),。

第三，用Excel做回歸分析

我們研究銷售Y和促銷費用X1的關(guān)系,，數(shù)據(jù)如下：

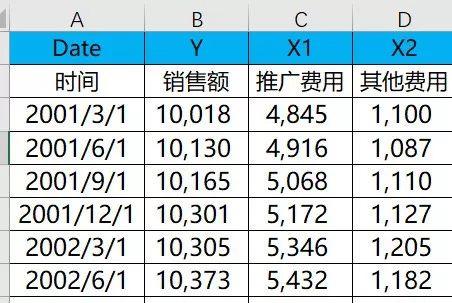
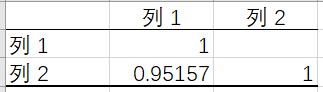
首先我們用數(shù)據(jù)分析——相關(guān)系數(shù)分析計算出自變量和因變量的相關(guān)系數(shù)為0.95157,，為強(qiáng)相關(guān)。

繪制如下散點圖：

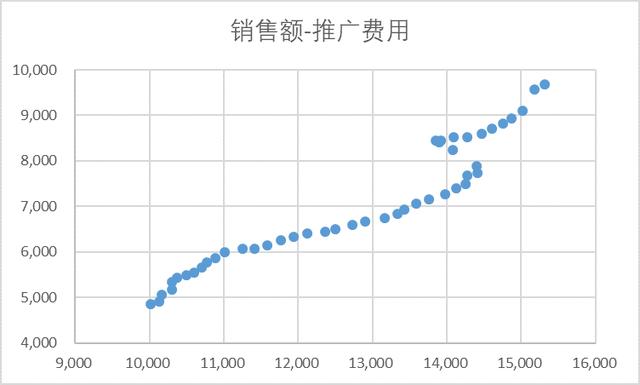
然后,，我們使用數(shù)據(jù)分析庫中的回歸進(jìn)行分析,。

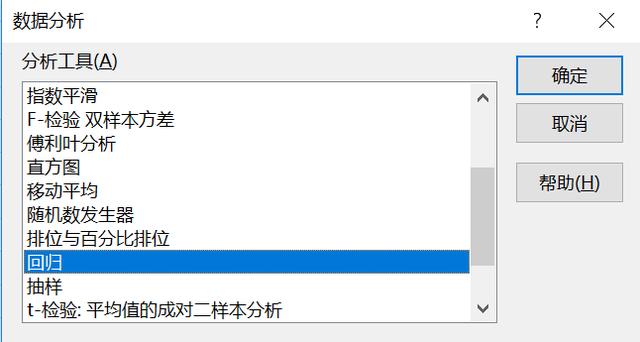
注意y值和x值的輸入?yún)^(qū)域，其中x值為自變量,，y為因變量,。

四、線性回歸方程的檢驗

評估回歸擬合的程度(重要),；

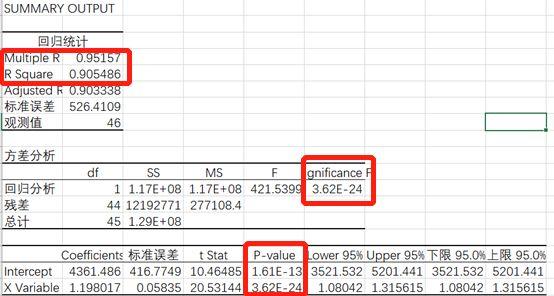
1.我們先來看回歸統(tǒng)計表,。倍數(shù)R是相關(guān)系數(shù)R的值，與我們之前相關(guān)分析得到的值相同,。大于0.8的值表示強(qiáng)正相關(guān),。

2.在回歸統(tǒng)計表中，R的平方是R的平方,，也可稱為決策系數(shù)和擬合優(yōu)度,，取值范圍為[0,，1]。R的平方越大,，模型的擬合度越好,。一般即使超過70%，低于60%也需要修改模型,。這種情況下,，R的平方是0.9054，相當(dāng)不錯,。

3.調(diào)整后的R是調(diào)整后的R平方,。該值用于修正因自變量個數(shù)增加導(dǎo)致模型擬合效果過高的情況，多用于度量多元線性回歸,。

4.第二個表,，方差分析表，說明df是自由度,，SS是平方和,，MS是均方，F(xiàn)是F統(tǒng)計量,，顯著性F是回歸方程總體的顯著性檢驗,，其中我們主要關(guān)注的是F檢驗的結(jié)果，即顯著性F值,，f檢驗主要檢驗因變量和自變量之間的線性關(guān)系是否滿足方差分析的要求

6.在第三表中,，我們重點介紹P值，即P值,，用于檢驗回歸方程系數(shù)的顯著性,，也叫T檢驗。t檢驗看P值,，P值是F在顯著性水平的臨界值(一般取P=0.01P或0.05),。一般用來衡量測試結(jié)果是否顯著。如果P值為0.05,，則結(jié)果不具有統(tǒng)計學(xué)意義,。t檢驗是看自變量對因變量的線性顯著性。如果自變量不顯著,，可以將其從模型中排除。

7.從第三表的第一列可以得到這個回歸模型的方程：y=4361.486 1.198017x,，然后對于每個輸入自變量X,，我們可以根據(jù)這個回歸方程預(yù)測因變量Y。

本文簡要總結(jié)了什么是回歸分析,，如何用excel做線性回歸分析,，如何評價回歸方程的擬合程度,。入門很簡單，精通還很遠(yuǎn),，我們都在學(xué),。